Roof gutters may be needed with livestock facilities to divert clean water from contaminated lot runoff and minimize the total quantity of waste effluent requiring proper disposal.
Clean-water runoff
It is estimated that the annual runoff from a 92-foot by 200-foot barn roof near Springfield, Mo., will average about 470,000 gallons. If allowed to be polluted by manure, this nearly one-half million gallons of previously clean water must be disposed of on land without producing runoff.
Uncontaminated roof water can be discharged into the waters of the state or stored for farm use, such as watering livestock. Frequently, dairy barns present special problems due to their huge roof areas, which require large gutters and downspout capacity.
Positioning gutters to reduce snow and ice slide failures may be a major consideration. If the building eave-line has a 2- to 3-percent slope, as is common on gutter-flushed buildings, gutter capacity is increased compared to gutters mounted nearly level. Most gutters are mounted level for appearance, but a slope of 1/16 inch per foot is desirable for drainage.
An alternative to roof gutters for buildings with at least a 12-inch overhang and where an open channel will not be polluted is a surfaced channel or a stone-lined, tile-drained ditch alongside of the building. Also, an open channel could conduct water from a small gutter with multiple downspouts.
General information
In typical construction, downspouts are spaced from 20 feet to 50 feet with a 60-foot maximum. The final routing of the roof water may determine whether a small gutter with many downspouts will be more feasible than a large gutter with few downspouts. House-sized gutters are readily available. But in many rural locations, specially formed gutters may be quite expensive. Gutter hangers are normally spaced 3 feet on center (o.c.), but 1.5 feet o.c. is recommended where ice and snow are long-lasting.
In an environment with broad temperature changes, the gutters need to move without being restrained by the hangers. An alternative is to build the gutter with shorter lengths, allowing a space between sections for expansion. Table 1 shows the thermal expansion/contraction of a 100-foot length of gutter with 100 degrees of temperature change.
Table 1
Coefficient of expansion and expansion/contraction of 100 feet of gutter with 100 degrees of temperature change
| Metal | Coefficient of expansion | Total movement |
|---|---|---|
| Aluminum | 0.0000128 | 1.54 inch |
| Copper | 0.0000093 | 1.12 inch |
| Galvanized steel | 0.0000065 | 0.78 inch |
Examples
This publication will work example problems to illustrate the use of roof gutters.
Example 1
Level gutters
Design a gutter/downspout system for a 92-foot by 200-foot free-stall barn located near Boonville, Mo., with a 4:12 gable roof. Assume a level rectangular gutter with a depth to width ratio of 0.75.
On the 200-foot-long roof, assume four downspouts. Use the factor of 1.05 from Table 2 to adjust the roof plan-area for the 4:12 roof pitch.
Table 2
Design-area adjustment factor for pitched roofs. Multiply the plan area of the roof by the adjustment factor corresponding to the roof pitch
| Roof pitch1 | Factor |
|---|---|
| Level to 3 inches per foot | 1.00 |
| 4 inches to 5 inches per foot | 1.05 |
| 6 inches to 8 inches per foot | 1.10 |
| 9 inches to 11 inches per foot | 1.20 |
| 12 inches per foot | 1.30 |
1When the roof is sloped, neither the plan area nor the actual roof area should be used in sizing drainage.
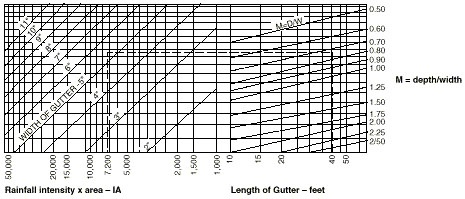 Figure 1
Figure 1
Width of level rectangular gutters for given roof areas and rainfall intensities.
Use Figure 1 to find the width of gutter for 50-foot lengths of gutter. Use the rainfall intensity value of 7.2 inches per hour for Boonville from Figure 2 . For a segment of roof 46 feet wide by 50 feet long, the adjusted "IA" value will be: IA = 46 feet x 50 feet x 1.05 x 7.2 = 17,388. From Figure 1, for a depth/width ratio of 0.75, the required gutter width is 7.5 inches. Select a rectangular gutter 8 inches wide by 6 inches deep.
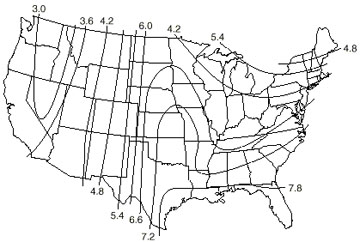 Figure 2
Figure 2
Map shows rainfall intensity in inches per hour for 5-minute periods to be expected once in 10 years. Normally, this is adequate for design, but storms have been twice as intense in some areas. See local records for more accurate data.
Example 2
Sloped gutters
Assume the foundation, eave height and gutter for the free-stall barn are sloped at 2 percent for flushing the alleys. To determine the width of a rectangular gutter, see Table 3. Refer to Table 4 to determine the diameter of a semi-circular gutter to carry runoff from a 50-foot long portion of the building.
Table 3
Capacity for rectangular roof gutters
| Depth of gutter = 0.75 x width. Capacities calculated using Manning's formula for open channel flow: Q = 1.486 x S 0.667) with n = 0.012 for smooth metal, smooth concrete or planed lumber and P = wetted perimeter in feet. | |||||
| Gutter width (inches) | Gutter slope (percent) | ||||
|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | |
| Capacity, (cubic feet per second) cfs | |||||
| 4 | 0.16 | 0.22 | 0.31 | 0.38 | 0.44 |
| 5 | 0.28 | 0.40 | 0.57 | 0.70 | 0.80 |
| 6 | 0.46 | 0.65 | 0.92 | 1.13 | 1.31 |
| 7 | 0.70 | 0.98 | 1.29 | 1.70 | 1.97 |
| 8 | 1.00 | 1.41 | 1.99 | 2.44 | 2.82 |
| 9 | 1.36 | 1.93 | 2.72 | 3.34 | 3.85 |
| 10 | 1.80 | 2.55 | 3.61 | 4.42 | 5.11 |
| 12 | 2.94 | 4.16 | 5.88 | 7.20 | 8.31 |
Table 4
Capacity for smooth semi-circular gutters, such as PVC, at various slopes
| Capacities calculated using Manning's formula for open channel flow: Q = 1.486 x S0.0667) with n = 0.010 and P = wetted perimeter in feet (flow depth = 50 percent of diameter). | |||||
| Gutter width (inches) | Gutter slope (percent) | ||||
|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | |
| Capacity, (cubic feet per second) cfs | |||||
| 4 | 0.07 | 0.10 | 0.14 | 0.17 | 0.20 |
| 5 | 0.13 | 0.18 | 0.25 | 0.31 | 0.36 |
| 6 | 0.20 | 0.29 | 0.41 | 0.50 | 0.58 |
| 8 | 0.44 | 0.62 | 0.88 | 1.08 | 1.24 |
| 10 | 0.80 | 1.13 | 1.60 | 1.96 | 2.26 |
| 12 | 1.30 | 1.84 | 2.60 | 3.18 | 3.67 |
First, determine the roof runoff:
| runoff rate = | 46 feet x 50 feet x 1.05* x 7.2 inches per hour 12 inches per foot x 3,600 seconds per hour | = 0.40 cfs |
*Roof area adjustment factor for 4:12 roof slopes.
Select a gutter with at least 0.40 cfs capacity at 2 percent slope. From Table 3, select a rectangular gutter 5 inches wide (depth = 0.75 times width = 3.75 inches). Select a semicircular gutter 6 inches in diameter (Table 4).
Example 3
Sizing downspouts
Select an adequate downspout to accommodate 0.40 cfs flow with 3.75-inch head from the rectangular gutter in Example 2.
In Table 5, we find that with a 3.75-inch head, a 6-inch diameter downspout will be required. Because the gutter is only 5 inches wide, a rectangular 5-inch by 6-inch transition may be used to connect the 6-inch round downspout to the 5-inch gutter.
Table 5
Capacity of circular downspouts based on orifice flow
| Use the orifice coefficient of 0.6 in the following formula: Q = CA (2gh)0.5 where A = cross-sectional area of downspout in square feet and h = head in feet. | ||||||
| Head (inches) | Downspout diameter (inches) | |||||
|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | |
| Capacity, cfs | ||||||
| 2 | 0.10 | 0.17 | 0.27 | 0.39 | 0.53 | 0.69 |
| 4 | 0.14 | 0.24 | 0.38 | 0.55 | 0.74 | 0.97 |
| 6 | 0.17 | 0.30 | 0.46 | 0.67 | 0.91 | 1.19 |
| 8 | 0.19 | 0.34 | 0.54 | 0.77 | 1.05 | 1.37 |
| 10 | 0.22 | 0.38 | 0.60 | 0.86 | 1.17 | 1.53 |
| 12 | 0.24 | 0.42 | 0.66 | 0.95 | 1.39 | 1.82 |
| 14 | 0.26 | 0.45 | 0.71 | 1.02 | 1.39 | 1.82 |
| 16 | 0.27 | 0.49 | 0.76 | 1.09 | 1.49 | 1.94 |
| 18 | 0.29 | 0.51 | 0.80 | 1.16 | 1.58 | 2.06 |
| 20 | 0.31 | 0.54 | 0.85 | 1.22 | 1.66 | 2.17 |
| 22 | 0.32 | 0.57 | 0.89 | 1.28 | 1.74 | 2.28 |
| 24 | 0.33 | 0.59 | 0.93 | 1.34 | 1.82 | 2.38 |
An alternative would be to increase the head above the 6-inch downspout by means of a drop box.
Downspout capacity
Downspout capacity can be increased by using a tapered transition to enlarge the downspout entrance in the bottom of the gutter, thus increasing the inlet area. Or you may add a dropbox at each downspout location to increase the head of water above the downspout entrance. See Table 5 for the capacity of various downspout diameter sizes at various heads.
A rule of thumb for sizing the tapered inlet or drop-box inlet is for the cross-sectional (horizontal) area to be at least 1.5 times the downspout cross-sectional area and the vertical drop from the gutter to the downspout entrance to be at least twice the downspout diameter.
Using the 0.40 cfs downspout capacity needed for the 50-foot sloped gutter in Example 2, determine the total head necessary to cause 0.40 cfs to enter a 4-inch diameter downspout.
From Table 5, by interpolation, we find that 11 inches of head will cause 0.40 cfs to enter the 4-inch downspout.
Using the rules of thumb above, we would select an 11-inch deep dropbox (or a tapered transition) with a horizontal area of at least 18.85 square inches. See the following formula:
Required area = 1.5 x 22(pi) = 1.5 x 12.56 = 18.85 square inches (pi = 3.14)
Clearance for snow and ice slides
Clearance for snow and ice slides should be taken into account in positioning the gutters. In general, the flatter the roof pitch, the greater the clearance required. Use Figure 3 as a guide in positioning gutters for the snow and ice clearance.
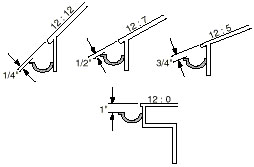 Figure 3
Figure 3
Properly position gutters. Snow and ice can slide off the roof clear of the gutter. Steeper pitch roofs require less clearance.
Standard downspouts
Table 6 provides data for selecting sizes for various shapes of standard downspouts, based on cross-sectional area.
Table 6
Standard downspout sizes
| Type | Area square (inches) | Nominal size (inches) | Actual size diameter (inches) |
|---|---|---|---|
| Plain round | 7.07 | 3 | 3 |
| 12.57 | 4 | 4 | |
| 19.63 | 5 | 5 | |
| 28.27 | 6 | 6 | |
| 5.94 | 3 | 3 | |
| Corrugated round | 11.04 | 4 | 4 |
| 17.72 | 5 | 5 | |
| 25.97 | 6 | 6 | |
| (depth x width) | |||
| Corrugated rectangular | 3.80 | 2 | 1-3/4 x 2-1/4 |
| 7.73 | 3 | 2-3/8 x 3-1/4 | |
| 11.70 | 4 | 2-3/4 x 4-1/4 | |
| 18.75 | 5 | 3-3/4 x 5 | |
| Plain Rectangular | 3.94 | 2 | 1-3/4 x 2-1/4 |
| 6.00 | 3 | 2 x 3 | |
| 12.00 | 4 | 3 x 4 | |
| 20.00 | 5 | 3-3/4 x 4-3/4 | |
| 24.00 | 6 | 4 x 6 | |
Discharging water onto erodible soil/sod
For small downspouts discharging water onto erosion-resistant surfaces, spreader/splash pans may be used (Figure 4).
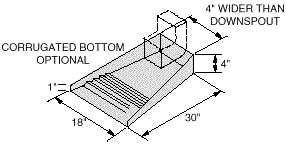 Figure 4
Figure 4
Spreader/splash pan for discharging downspouts onto erosion-resistant surfaces.
Discharging large downspouts or conduits receiving water from several downspouts onto soil may require special treatment to prevent erosion or to eliminate a plunge pool.
Typically, discharges from large gutters may be routed via an underground or overland pipe to a stable channel or via a surface channel to a grass waterway or a rock-lined channel. Table 7 gives suggested permissible discharge velocities to use if more specific values are not available for bare and vegetated waterways. Table 8 contains data for flow in trapezoidal channels with recommended 4:1 side slopes.
Table 7
Maximum permissible water velocities to prevent erosion in grassy waterways
| More erodible soils1 | Less erodible soils2 | |||||
|---|---|---|---|---|---|---|
| Percent slope | Percent slope | |||||
| 0 to 5 | 6 to 10 | more than 10 | 0 to 5 | 6 to 10 | more than 10 | |
| Cover | (Velocity, feet per second) | |||||
| None | ||||||
| Cultivated | 1.5 | NR3 | NR | 2.5 | NR | NR |
| Not cultivated | 2.0 | NR | NR | 2.5 | NR | NR |
| Annual grasses and legumes | ||||||
| Sparse stand | 2.5 | NR | NR | 3.0 | NR | NR |
| Good stand | 3.0 | NR | NR | 3.5 | NR | NR |
| Average-density grasses (bluegrass, fescue and brome) | ||||||
| Fair stand | 3.0 | 2.5 | 4 | 4.0 | 3.0 | 2.5 |
| Good stand | 4.0 | 3.5 | 3.0 | 5.0 | 4.0 | 3.5 |
| Excellent stand | 5.0 | 4.5 | 4.0 | 6.0 | 5.0 | 4.5 |
| Dense sod grasses (Bermuda) | ||||||
| Excellent stand | 6.0 | 5.0 | 4.0 | 7.0 | 6.0 | 5.0 |
1More erodible soils generally have a high content of fine sand or silt and lower plasticity. Typical soil textures are fine sand, silt, sandy loam and silty loam.
2Less erodible soils generally have a higher clay content and higher plasticity. Typical soil textures are silty clay, sandy clay and clay.
3NR — Not recommended.
4Must have good quality vegetation on these slopes.
Table 8
Maximum channel capacity and flow depth (for a trapezoidal channel with 4:1 side slopes) for various values of channel width, slope and "n," using Manning's formula with selected slopes and allowable velocities from Table 7 (table is split into two parts)
| Manning's formula for an open channel: V = (1.49/n) R0.5 where V = velocity in fps. R = the hydraulic radius in feet and s = the hydraulic gradient in feet per foot. In this table, velocity = 2 feet per second for non-vegetative, uncultivated waterways (n = 0.022) and velocities for vegetated waterways = 3, 4 and 5 feet per second (n = 0.04). | ||||
| Slope/velocity1 | Channel width (feet) | |||
|---|---|---|---|---|
| 2.0 | 4.0 | 6.0 | 8.0 | |
| Channel capacity in cfs per channel depth (feet) | ||||
| 1/2 | 1.3/0.2 | 1.8/0.2 | 2.3/0.2 | 2.9/0.2 |
| 1/3 | 28/1.3 | 30/1.1 | 32/1 | 36/1 |
| 1/4 | 88/2.1 | 88/1.9 | 91/1.8 | 96/1.6 |
| 1/5 | 211/3.0 | 214/2.8 | 212/2.6 | 226/2.5 |
| 3/2 | 0.37/0.1 | 0.64/0.1 | 0.95/0.1 | 1.3/0.1 |
| 3/3 | 5.6/0.5 | 7.2/0.4 | 8.9/0.4 | 10/0.4 |
| 3/4 | 16/0.8 | 19/0.7 | 22/0.6 | 25/0.6 |
| 3/5 | 41/1.2 | 43/1 | 47/1 | 52/0.9 |
| 5/2 | 0.25/0.1 | 0.42/0.1 | 0.62/0.1 | 0.83/0.1 |
| 5/3 | 2.9/0.3 | 3.9/0.3 | 5.2/0.3 | 6.4/0.2 |
| 5/4 | 8.5/0.5 | 10/0.4 | 13/0.4 | 16/0.4 |
| 5/5 | 20/0.8 | 22/0.7 | 25/0.6 | 29/0.6 |
| 8/2 | 0.15/0.03 | 0.29/0.03 | 0.43/0.03 | 0.58/0.03 |
| 8/3 | 1.7/0.2 | 2.6/0.2 | 3.3/0.2 | 4.3/0.2 |
| 8/4 | 4.6/0.3 | 6/0.3 | 7.6/0.3 | 9.3/0.3 |
| 8/5 | 10/0.5 | 13/0.4 | 15/0.4 | 18/0.4 |
| 10/2 | 0.13/0.03 | 0.25/0.03 | 0.37/0.03 | 0.5/0.03 |
| 10/3 | 1.3/0.2 | 2/0.1 | 2.8/0.1 | 3.6/0.1 |
| 10/4 | 3.3/0.3 | 4.8/0.2 | 6.4/0.2 | 7.8/0.2 |
| 10/5 | 7.5/0.4 | 9.4/0.3 | 12/3 | 15/0.3 |
1Slope in percent/velocity in feet per second.
Table 8
Maximum channel capacity and flow depth (for a trapezoidal channel with 4:1 side slopes) for various values of channel width, slope and "n," using Manning's formula with selected slopes and allowable velocities from Table 7 (continued)
| Manning's formula for an open channel: V = (1.49/n) R0.5 where V = velocity in fps. R = the hydraulic radius in feet and s = the hydraulic gradient in feet per foot. In this table, velocity = 2 feet per second for non-vegetative, uncultivated waterways (n = 0.022) and velocities for vegetated waterways = 3, 4 and 5 feet per second (n = 0.04). | |||
| Slope/velocity1 | Channel width (feet) | ||
|---|---|---|---|
| 10.0 | 12.0 | 14.0 | |
| Channel capacity in cfs per channel depth (feet) | |||
| 1/2 | 3.6/0.2 | 4.3/0.2 | 5/0.2 |
| 1/3 | 40/0.9 | 42/0.9 | 48/0.9 |
| 1/4 | 106/1.6 | 107/1.5 | 121/1.5 |
| 1/5 | 237/2.4 | 245/2.3 | 251/2.2 |
| 3/2 | 1.6/0.1 | 1.7/0.1 | 2/0.1 |
| 3/3 | 13/0.4 | 14/0.3 | 16/0.3 |
| 3/4 | 28/0.6 | 33/0.6 | 36/0.6 |
| 3/5 | 57/0.9 | 64/0.8 | 71/0.8 |
| 5/2 | 1/0.1 | 1.2/0.1 | 1.4/0.1 |
| 5/3 | 8/0.2 | 8.8/0.2 | 10/0.2 |
| 5/4 | 17/0.4 | 20/0.4 | 23/0.4 |
| 5/5 | 33/0.6 | 38/0.5 | 44/0.5 |
| 8/2 | 0.72/0.03 | 0.78/0.03 | 0.91/0.03 |
| 8/3 | 5.1/0.2 | 6/0.2 | 7/0.2 |
| 8/4 | 12/0.3 | 13/0.3 | 15/0.3 |
| 8/5 | 21/0.4 | 25/0.4 | 28/0.4 |
| 10/2 | 0.62/0.03 | 0.74/0.03 | 0.87/0.03 |
| 10/3 | 4.3/0.1 | 5.1/0.1 | 6/0.1 |
| 10/4 | 9.3/0.2 | 11/0.2 | 12/0.2 |
| 10/5 | 17/0.3 | 20/0.3 | 23/0.3 |
1Slope in percent/velocity in feet per second.
Some means of spreading the discharging water uniformly over a wide vegetated waterway is required. A suggested method is to use a gated discharge pipe in a concrete basin across the width of the flat bottom of a trapezoidal waterway (Figure 5). Data for selected gated discharge pipes are tabulated in Table 9.
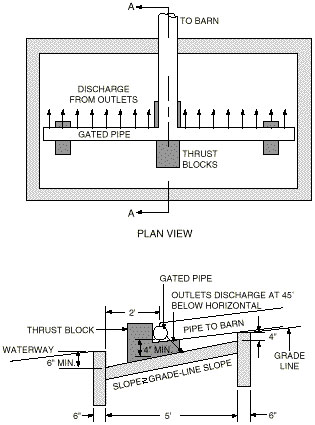 Figure 5
Figure 5
Schematic drawing of gated pipe in a concrete distribution basin discharging into a trapezoidal waterway.
Other types of energy-dissipating structures are shown in Soil and Water Conservation Engineering (References). One alternative is discharging water into a bed of large rocks to dissipate the energy and spread the flow.
For more information on the design of grassy waterways, consult your local Natural Resources Conservation Service (NRCS) office or your local MU Extension agricultural engineering specialist (you may get that person's name at your local MU Extension center).
Example 4
Waterway and distribution system
Select a waterway and distribution system to receive the roof discharge from a 92-foot by 200-foot barn with 4:12 roof slope. Determine the roof runoff (as shown previously):
| runoff rate = | 92 feet x 200 feet x 1.05* x 7.2 inches per hour 12 inches per foot x 3,600 seconds per hour | = 3.22 cfs |
*Roof area adjustment factor for 4:12 roof slopes.
Select the bottom width for a trapezoidal waterway on an 8-percent slope with a good stand of fescue. Table 7 shows the allowable waterway velocity is 3.5 feet per second. From Table 8, we see that a 4-foot-wide waterway will carry 2.6 cfs on an 8-percent slope at a velocity of 3 feet per second and 6 cfs at 4 feet per second on an 8-percent slope. By straight-line interpolation, the capacity of a 4-foot waterway at 3.5 feet per second would be a 4.3 cfs, adequate for the 3.22 cfs roof runoff. Note that the bottom width of a trapezoidal waterway channel may be chosen based on the width of equipment used for construction or for mowing and removing the grass instead of the minimum width necessary to achieve a non-erodible velocity.
Use Table 9 to select a distribution system with a 4-foot width and capacity of 3.22 cfs. A 4-foot distribution system with 5-inch diameter pipe, 12 holes that are 2 inches in diameter and 5.2 feet of head will result in a 3.2 cfs flow rate — just adequate for the maximum flow.
Table 9
Discharge data for gated distribution pipe
| Pipe diameter (inches)1 | Outlet diameter (inches) | Outlet flow rate (GPM) | Outlet flow variation (percent) | Number outlets | Total flow (CFS per GPM) | Head required (feet) |
|---|---|---|---|---|---|---|
| For 2-foot distribution pipe | ||||||
| 2 | 0.563 | 10 | 1 | 6 | 0.13/60 | 7.1 |
| 2 | 1.00 | 30 | 6 | 6 | 0.40/180 | 5.8 |
| 2 | 1.31 | 50 | 19 | 6 | 0.67/3,600 | 4.1 |
| 3 | 1.56 | 70 | 7 | 6 | 0.93/420 | 5.1 |
| 4 | 1.88 | 100 | 5 | 6 | 1.33/600 | 5.3 |
| 4 | 2.00 | 120 | 6 | 6 | 1.6/720 | 5.8 |
| 4 | 2.25 | 150 | 10 | 6 | 2/900 | 5.2 |
| 5 | 2.50 | 200 | 6 | 6 | 2.67/1,200 | 6.5 |
| 5 | 3.00 | 250 | 13 | 6 | 3.33/1,500 | 4.2 |
| 6 | 3.25 | 300 | 9 | 6 | 4/1,800 | 4.9 |
| For 4-foot distribution pipe | ||||||
| 2 | 0.563 | 10 | 3 | 12 | 0.27/120 | 6.8 |
| 3 | 1.06 | 30 | 8 | 12 | 0.8/360 | 4.4 |
| 3 | 1.31 | 50 | 21 | 12 | 1.33/600 | 4.3 |
| 4 | 1.56 | 70 | 13 | 12 | 1.87/840 | 4.8 |
| 4 | 1.88 | 100 | 29 | 12 | 2.67/1,200 | 3.7 |
| 5 | 2.00 | 120 | 14 | 12 | 3.2/1,440 | 5.2 |
| 5 | 2.25 | 150 | 24 | 12 | 4/1,800 | 4.3 |
| 6 | 2.50 | 200 | 17 | 12 | 5.3/2,400 | 5.7 |
| 6 | 2.75 | 250 | 27 | 12 | 6.7/3,000 | 5.2 |
| 7 | 3.0 | 300 | 19 | 12 | 8/3,600 | 5.9 |
| For 6-foot distribution pipe | ||||||
| 2 | 0.563 | 10 | 7 | 18 | 0.4/180 | 6.5 |
| 3 | 1.00 | 30 | 16 | 18 | 1.2/540 | 5.1 |
| 4 | 1.31 | 50 | 15 | 18 | 2/900 | 4.8 |
| 4 | 1.56 | 70 | 35 | 18 | 2.8/1,260 | 3.6 |
| 6 | 1.88 | 100 | 13 | 18 | 4/1,800 | 4.8 |
| 6 | 2.00 | 120 | 17 | 18 | 4.8/2,160 | 5.1 |
| 6 | 2.25 | 150 | 29 | 18 | 6/2,700 | 4.2 |
| 8 | 2.62 | 200 | 16 | 18 | 8/3,600 | 4.8 |
| 8 | 2.943 | 250 | 27 | 18 | 10/4,500 | 4.1 |
| 8 | 3.00 | 300 | 30 | 18 | 12/5,400 | 5.3 |
| For 8-foot distribution pipe | ||||||
| 2 | 0.563 | 10 | 13 | 24 | 0.53/240 | 6.0 |
| 4 | 1.00 | 30 | 9 | 24 | 1.6/720 | 5.7 |
| 4 | 1.31 | 50 | 31 | 24 | 2.67/1,200 | 4.0 |
| 6 | 1.56 | 70 | 11 | 24 | 3.7/1,680 | 5.1 |
| 6 | 1.88 | 100 | 25 | 24 | 5.33/2,400 | 4.2 |
| 8 | 2.06 | 120 | 11 | 24 | 6.4/2,880 | 4.9 |
| 8 | 2.25 | 150 | 16 | 24 | 8/3,600 | 5.1 |
| 8 | 2.62 | 200 | 33 | 24 | 10.7/4,800 | 3.9 |
| 10 | 2.94 | 250 | 19 | 24 | 13.3/6,000 | 4.6 |
| 10 | 3.25 | 300 | 32 | 24 | 16/7,200 | 3.8 |
| For 10-foot distribution pipe | ||||||
| 2 | 0.563 | 10 | 22 | 30 | 0.67/300 | 5.4 |
| 4 | 1.00 | 30 | 15 | 30 | 2/900 | 5.3 |
| 6 | 1.31 | 50 | 9 | 30 | 3.33/1,500 | 5.4 |
| 6 | 1.56 | 70 | 18 | 30 | 4.67/2,100 | 4.6 |
| 8 | 1.88 | 100 | 12 | 30 | 6.67/3,000 | 4.9 |
| 8 | 2.06 | 120 | 18 | 30 | 8/3,600 | 4.5 |
| 8 | 2.25 | 150 | 27 | 30 | 10/4,500 | 4.4 |
| 10 | 2.62 | 200 | 20 | 30 | 13.3/6,000 | 4.7 |
| 12 | 2.94 | 250 | 15 | 30 | 16.7/7,500 | 4.9 |
| 12 | 3.25 | 300 | 23 | 30 | 20/9,000 | 4.3 |
| For 12-foot distribution pipe | ||||||
| 3 | 0.625 | 10 | 9 | 36 | 0.80/360 | 4.1 |
| 4 | 1.00 | 30 | 23 | 36 | 2.4/1,080 | 4.7 |
| 6 | 1.31 | 50 | 13 | 36 | 4/1,800 | 5.1 |
| 6 | 1.56 | 70 | 28 | 36 | 5.6/2,520 | 4.1 |
| 8 | 1.88 | 100 | 18 | 36 | 8/3,600 | 4.6 |
| 8 | 2.00 | 120 | 24 | 36 | 9.6/4,320 | 4.8 |
| 10 | 2.25 | 150 | 15 | 36 | 12/5,400 | 5.2 |
| 10 | 2.62 | 200 | 31 | 36 | 16/7,200 | 4.1 |
| 12 | 2.94 | 250 | 22 | 36 | 20/9,000 | 4.5 |
| 12 | 3.25 | 300 | 36 | 36 | 24/10,800 | 3.7 |
| For 14-foot distribution pipe | ||||||
| 3 | 0.613 | 10 | 12 | 42 | 0.93/420 | 4.3 |
| 4 | 1.00 | 30 | 32 | 42 | 2.8/1,260 | 4.4 |
| 6 | 1.31 | 50 | 18 | 42 | 4.67/2,100 | 4.8 |
| 6 | 1.44 | 70 | 28 | 42 | 6.53/2,940 | 5.8 |
| 8 | 1.88 | 100 | 25 | 42 | 9.33/4,200 | 4.2 |
| 8 | 2.00 | 120 | 35 | 42 | 11.2/5,040 | 4.2 |
| 10 | 2.25 | 150 | 22 | 42 | 14/6,300 | 4.7 |
| 12 | 2.56 | 200 | 17 | 42 | 18.7/8,400 | 5.3 |
| 12 | 2.94 | 250 | 32 | 42 | 23.3/10,500 | 4.0 |
| 12 | 3.00 | 300 | 36 | 42 | 28/12,600 | 5.1 |
1Pipe diameter is based on distribution pipe being center-fed. If pipe is end-fed, pipe size will need to be increased substantially.
If the slope from the barn to the distribution pipe is also 8 percent, from Table 10 we find that a 4-inch PVC pipe will be adequate for conveying the 3.22 cfs flow from the barn to the gated distribution pipe. However, to have a residual head of at least 5.2 feet at a gated distribution pipe (as opposed to an open discharge pipe, as in Table 10), the pressure drop through the conduit from the barn should be investigated and the conduit should be sized to provide adequate pressure at the distribution point.
Table 10
Gravity flow for smooth pipes, such as PVC, at various slopes
| Manning's formula for open channel flow: Q = 1.486 x S0.667) with n = 0.010 and P = wetted perimeter in feet (flow depth = 70 percent of diameter). | |||||||
| Slope (percent) | Pipe diameter (inches) | ||||||
|---|---|---|---|---|---|---|---|
| 4 | 5 | 6 | 8 | 10 | 12 | ||
| Capacity (cfs) | |||||||
| 0.5 | 0.12 | 0.22 | 0.36 | 0.78 | 1.41 | 2.29 | |
| 1 | 0.17 | 0.31 | 0.51 | 1.10 | 1.99 | 3.24 | |
| 2 | 0.24 | 0.44 | 0.72 | 1.56 | 2.82 | 4.59 | |
| 3 | 0.30 | 0.54 | 0.88 | 1.90 | 3.45 | 5.62 | |
| 4 | 0.35 | 0.63 | 1.02 | 2.20 | 3.99 | 6.48 | |
| 5 | 0.39 | 0.70 | 1.14 | 2.46 | 4.46 | 7.25 | |
| 6 | 0.42 | 0.77 | 1.25 | 2.69 | 4.88 | 7.94 | |
| 8 | 0.49 | 0.89 | 1.44 | 3.11 | 5.64 | 9.17 | |
| 10 | 0.55 | 0.99 | 1.62 | 3.48 | 6.31 | 10.26 | |
| 12 | 0.60 | 1.09 | 1.77 | 3.81 | 6.91 | 11.23 | |
| 14 | 0.65 | 1.18 | 1.91 | 4.12 | 7.46 | 12.13 | |
| 16 | 0.69 | 1.26 | 2.04 | 4.40 | 7.98 | 12.97 | |
For more information on the design of gated-pipe systems, consult your local NRCS area engineer or your MU Extension regional agricultural engineering specialist. You may get that person's name from your local NRCS office or local MU Extension center). The engineers have a computer program available for design of gated-pipe systems.
Pipes to carry water from downspouts
Downspouts can be discharged into a pipe suspended on the side of the building at some design slope, laid on the ground alongside the building or buried underground at the design slope. Use Table 10 to select the pipe size based on the required capacity and the pipe slope. The capacities are based on water flowing in the pipe at a depth equal to 70 percent of the inside pipe diameter.
References
- American Institute of Architects, Architectural Graphics Standards, eighth edition. 1988, John Wiley and Sons, Inc., New York.
- Beasley, R.P., Gregory, J.M. and McCarty, T.R., Erosion and Sediment Pollution Control, Second Edition. Iowa State University Press, Ames, Iowa.
- Schwab, G.O., et. al., Soil and Water Conservation Engineering. 1981, John Wiley and Sons, New York.